In this Post ...

I'll show how I applied some simple trigonometry to create a seamless billowing effect using SVG and requestAnimationFrame. Then, as an added bonus I'll provide a tool for the SVG Creators Collaborative to make SVG waves for creating similar effects.

Introduction

Not long ago I published a post on animating Scalable Vector Graphics (SVG) with javascript's requestAnimationFrame framework. In that post, I illustrated the technique of sprite-based frame-by-frame animation by animating the cape on a character inspired by Frank Baum's wicked witch of the west.

When I published that post, I sort of promised some more details on the techniques I used to acheive the billowing effect and, well, here we are.

Animation Effects Inspired by Math

I created the billowing effect on the wicked witch sprite using key-frame animation with frame swaps. In other words, the animation is analogous to traditional hand-drawn animation where separate drawings are created to be shown on a fixed interval at a rate that for the human eye achieves apparent motion. But in order to achieve a good effect, you can't just randomly draw a bunch if images. To get good apparent motion you have to simulate real motion. You have to impose some order on the chaos.

The billow-effect is one of a broader class of effects arising due to the wind element. Artists know you can't actually draw wind. But you can get good compelling art if you can draw its effect. Faced with this problem, I tried a couple of times to get a good billow -- only to realize it's not so trivial! Even if they're not always adept at saying why, human beings are pretty good at discriminating between believable animation and models that just don't make sense. That's key. Experienced animators agree that the key to distinguishing poor quality cheap animation from amazing animated art experiences is understanding how things behave.

So finally I realized that billowing cloth -- and many other effects ranging from waves on the sea surface to reeds bending in the wind -- can be modeled with a little basic trigonometry ¹ . So what follows is the formula that I applied to get the effect I was after.

Here's the Math

You don't have to be a math wiz to understand what a wave is. Nevertheless, It may be a while since you've sat through a math class so here's a quick refresher that'll bring back everything you need.

Figure 2: Anatomy of a sine wave. This figure shows a graph of $y=sin(x)$ denoting wavelength, period, and amplitude of the wave.

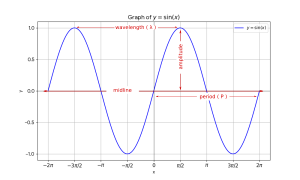
Figure two illustrates the anatomy of a sine wave. I've called out the key features; namely the period, amplitude and wavelength.

1. The period is the duration of the wave (i.e., the amount of time it takes the wave to traverse the length of a cycle).

2. The amplitude is the difference between the peak and the midline.

3. And finally I've labeled the wavelength ($\lambda$) which is the spatial distance spanning one cycle. ²

So with this in mind I simply modeled the billowing cape by sliding a wave like this across the hem of the cape. Believe it or not, understanding and using this technique can make life much much easier when you want to create these kinds of animation effects.

For a resting state animation the artist is looking for something that will loop seamlessly. You don't want a jarring discontinuity on every cycle of your loop. Instead of just guessing at it, it pays off to do some quick calculations up front. And here's how.

The formula.

Sliding the wave essentially amounts to traveling a sinusoid. In other words, we want to slide the sine wave across the viewport window like so:

Let's start with the general equation for a traveling wave.

$$ y(x, t) = \sin\left(\frac{2\pi(x - vt)}{P}\right) $$

Don't panic! All you need to know to use this are the parameters you can tweak -- the levers you can pull to get your wave. So to make your wave you all you need is:

1. $P$ (the period), and

2. The range for x

Since we only need the initial state of the waveform to use it for our effect we can hold time ($t$) constant at 0 (which cancels out velocity ($v$)). As described above, you can think of the period here spatially (same as wavelength) -- with pixels being the unit of measure. Given that, we can draw a sine wave for any range in x (i.e., length in pixels).

Example

Back to our wicked sprite, let's use her as an example. Again I created the sprite in a 50 X 50 bounding box. So let's just set the period:

1. Let P = 50.

And I want a wave to travel across that bounding box. So to make the visiualiztion easier I'll draw two periods and pull the start point back by the length of one:

1. Let x-range = [-50, 50]

You can visualize the resultant wave if you play with the tool I've inlined below.

Applying the waveform.

But remember ...

The goal is to travel the wave across several frames, such that after a certain number them the wave returns to its initial position -- effectively creating a perfect loop.

In order to achieve that we still need the amount by which to displace the wave on each frame. For that we need $v$ from the equation; the wave's velocity ($v$) per frame. And with this approach, that's easy to get, simply divide the period, $P$, by the number of frames in the loop:

$$ v = \frac{P}{number \hspace{1mm} of \hspace{1mm} frames} $$

Soooo for the wicked sprite:

The Visualization

Below I've reproduced the key frames I created for the billowing effect on Ms. Witch. I've highlighted the hem of the cape where if you look close you can visualize the form of the sinusoid as it's traveled across the the viewport.

Figure: Keyframes used to achieve the billowing effect on the witch's cape. Notice how I sculpted the hem to conform to the sinusoidal curve travelled across the viewport.

Bonus! Here's the Tool

And finally, here's the tool I promised for the SVG Collab™. To use the tool, simply tweak the parameters to generate your wave and copy the result to your clipboard. When you do the copy you'll get an SVG path of the form:

<path id="sineWavePath" fill="none" stroke="red" stroke-width="1" d="M -50 -6.123233995736766e-15 L -49.5 -1.5697629882328317 ..."> </path>

Simply drop it your SVG document and take it from there. Use it in good health!

Discussion

In this post I explained an approach to creating SVG animation effects inspired by trigonometry. Without a doubt, drawing out the many keys required for key frame animation is always time consuming, and can be downright excruciating. And relying solely on intuition to dream up effects like billowing cloth can lead to nothing but frustration at the end of the day.

So, rather than randomly render a bunch of cells only to end up with an effect that doesn't make visual sense, why not apply a little math and get a much better outcome in the end. Drawing animation frames can take many many hours of effort. Use a little math and get it right the first time!

The technique I've exemplified in this post can be used in SVG, canvas animations, or WebGL shaders -- anywhere basically where you want to simulate smooth, cyclical motion. It's simple, efficient, and math-driven, which keeps your animation clean and loopable. Use it in good health!

In conclusion let me leave you with this thought. For many people, math can be intimidating. Especially if you're under the pressure of an educational system that values competition over cooperation and crams exams down your throat in order to filter the "haves" from the "have nots" to create a class of "gonna gets". But if you can overcome the trauma induced by a broken system to embrace mathematics you can absolutely use it to your advantage to create beautiful artworks!

Endnotes

1. For many, math is a "four-letter word". Believe me I understand that initial aversion. However, I truly hope you'll look past any fear of terms like trigonometry. It's my absolute favorite math, and my experience has shown me time and time again how powerful even a basic grasp of trig can be in crafting remarkable and beautiful works of art .

2. At first glance it's easy to conflate the period of a wave with the concept of wavelength and, indeed, the concepts are closely related. But there's a subtle distinction that can become important. While both describe aspects of a repeating wave cycles, they refer to different dimensions :

   • Wavelength ($\lambda$) is a spatial measurement. It's the distance a wave covers in one complete cycle. If you are creating an effect like ripples on a pond you're thinking spatially and talking wavelength.

   • The Period (T) is a temporal measurement. It's the time that it takes for one complete cycle of a wave to pass a fixed point. In creating the billowing effect we're concerned with the time it takes a wave to move across a fixed interval so I've used the term period to describe the length of the cycle .

Resources

1. Sine Waves from Libre Texts

2. Wave Principle in Inkscape

3. SVG Creators Collaborative&trade -- Sine Wave Generator